Bài 93 Toán lớp 4 giới thiệu về hình bình hành và cách tính chu vi, diện tích của nó. Dưới đây là hướng dẫn chi tiết giúp các em nắm vững kiến thức và áp dụng vào bài tập.

1. Lý thuyết hình bình hành Toán lớp 4
1.1. Khái niệm và đặc điểm hình bình hành
Hình bình hành là một trong những hình học phổ biến, không chỉ tồn tại trong lĩnh vực toán học mà còn được sử dụng rộng rãi trong cuộc sống thực tế. Để hiểu sâu hơn về kiến thức hình học này và để giúp đỡ việc học tập của bạn trở nên hiệu quả, dưới đây là một số thông tin chi tiết.
Hình hình hành được biết đến là một loại tứ giác đặc biệt, được hình thành bởi hai cặp cạnh song song và cắt nhau. Đồng thời, nó cũng là một hình học tứ giác đều có tổng cộng 4 góc và một số tính chất tương tự với hình chữ nhật và hình thang.
Dưới đây là một số tính chất cơ bản của hình bình hành:
- Các cạnh đối diện trong hình bình hành là song song và có độ dài bằng nhau.
- Các góc đối diện trong hình bình hành có độ đo bằng nhau.
- Hai đường chéo trong hình bình hành luôn cắt nhau tại trung điểm của mỗi đường.
Đây là những điểm quan trọng để hiểu về hình hành và áp dụng chúng trong các bài toán hình học.
Dấu hiệu nhận biết Hình bình hành:
Để có thể xác định một hình là hình bình hành trong nhiều hình học khác, ta có thể nhận biết dựa trên các đặc điểm sau đây:
- Nếu tứ giác có các cạnh đối diện là song song, thì đó là hình bình hành. Ví dụ: Tứ giác ABCD có AB//CD và AD//CB, thì ABCD là hình bình hành.
- Nếu tứ giác có các cạnh đối diện có độ dài bằng nhau, thì đó là hình bình hành. Ví dụ: Tứ giác ABCD có AB = CD, AD = BC, thì ABCD là hình bình hành.
- Nếu tứ giác có hai cạnh đối diện là song song và có độ dài bằng nhau, thì đó cũng là hình bình hành. Ví dụ: Tứ giác ABCD có AB//CD và AB = CD, hoặc AD//BC và AD = BC, thì ABCD là hình bình hành.
- Nếu tứ giác có các góc đối diện bằng nhau, thì đó là hình bình hành.
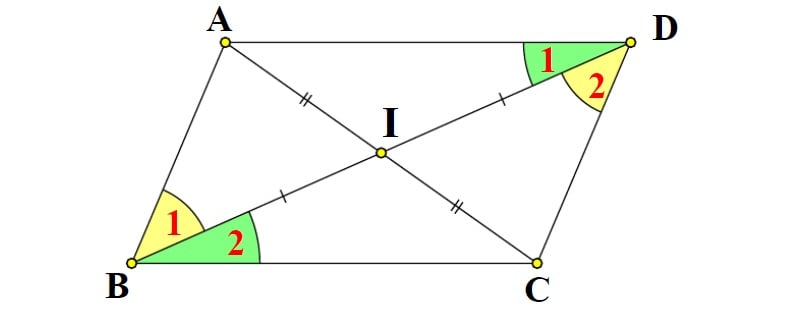
- Nếu tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường chéo và độ dài của chúng bằng nhau, thì đó là hình bình hành. Ví dụ: Tứ giác ABCD có đoạn chéo AC cắt đoạn chéo BD tại điểm O. Nếu OA = OC và OB = OD, thì ABCD là hình bình hành.
1.2. Các công thức liên quan tới Hình bình hành
Trong chương trình học toán lớp 4, các em sẽ bắt đầu làm quen với hình học, cùng với đó là việc học các công thức tính toán liên quan như sau:
Chu vi hình bình hành:
Để tính chu vi hình bình hành, ta có thể dùng hai cách. Cách đầu tiên là tính tổng độ dài của 4 cạnh bao quanh hình. Cách thứ hai là tính 2 lần tổng độ dài của bất kỳ cặp cạnh kề nhau.
Công thức cụ thể như sau: Chu vi (C) = 2 x (a + b)
Trong đó:
- C là chu vi của hình bình hành.
- a và b là độ dài của hai cạnh kề nhau của hình bình hành.
Diện tích hình bình hành:
Diện tích hình bình hành được tính bằng cách nhân độ dài của cạnh đáy (a) với chiều cao (h) nối từ đỉnh xuống đáy của hình.
Công thức cụ thể như sau: Diện tích (S) = a x h
Trong đó:
- S là diện tích của hình bình hành.
- a là độ dài của cạnh đáy của hình bình hành.
- h là chiều cao từ đỉnh tới đáy của hình bình hành.
2. Các dạng toán về hình bình hành tiểu học thường gặp
Trong chương trình học toán lớp 4, phần hình học sẽ giới thiệu các dạng bài tập cơ bản sau đây:
Dạng 1: Công thức định nghĩa
Phương pháp giải: Dạng toán này yêu cầu các em nắm vững các khái niệm, tính chất, và dấu hiệu nhận biết để đưa ra đáp án chính xác.
Ví dụ: Trong các tứ giác sau, tứ giác nào là hình bình hành? Vì sao?
Hướng dẫn:
a) Tứ giác ABCD có AB = CD và BC = AD, do đó ABCD là hình bình hành.
b) Tứ giác ABCD có cạnh đối song song và bằng nhau, do đó ABCD là hình bình hành.
c) Tứ giác ABCD có cạnh đối không song song và không bằng nhau, suy ra ABCD không phải hình bình hành.
d) Tứ giác ABCD có hai đường chéo AC và BD. AC giao BD tại O. Ta có: OA = OC, OB = OD, suy ra ABCD là hình bình hành.
e) Tứ giác ABCD có cạnh đối song song và bằng nhau, do đó ABCD là hình bình hành.
Dạng 2: Tính chu vi hình bình hành
Phương pháp giải: Các em sẽ sử dụng công thức C = 2 x (a + b) để tính chu vi của hình.
Ví dụ: Cho hình bình hành ABCD có hai cạnh a và b lần lượt là 3 cm và 5 cm. Hỏi chu vi của hình bình hành ABCD bằng bao nhiêu?
Đáp án: Chu vi của hình bình hành ABCD là:
C = (a + b) x 2 = (3 + 5) x 2 = 16 cm
Dạng 3: Tính diện tích hình bình hành
Phương pháp giải: Ta sẽ sử dụng công thức tính diện tích S = a x h để giải toán.
Ví dụ: Hình bình hành ABCD có chiều cao cạnh đáy CD là 5 cm và chiều cao nối từ đỉnh A xuống cạnh đáy CD là 3 cm. Tính diện tích hình bình hành ABCD?
Đáp án: Diện tích của hình bình hành là:
S = a x h = 5 cm x 3 cm = 15 cm2
3. Bài 93 Hình bình hành: Vở bài tập Toán lớp 4
Giải vở bài tập Toán lớp 4 tập 2 trang 10 - Bài 1
Viết tên mỗi hình vào chỗ chấm:
.png)
Đáp án:
.png)
Giải vở bài tập Toán lớp 4 tập 2 trang 11 - Bài 2
Cho các hình sau:
Viết các chữ “có” hoặc “không” vào các ô trống của bảng sau:
| Đặc điểm | (1) | (2) | (3) | (4) | (5) |
| Có 4 cạnh và 4 góc | |||||
| Có hai cặp cạnh đối diện song song | |||||
| Có hai cặp cạnh đối diện bằng nhau | |||||
| Có 4 góc vuông và 4 cạnh bằng nhau | |||||
Đáp án
| Đặc điểm | (1) | (2) | (3) | (4) | (5) |
| Có 4 cạnh và 4 góc | Có | Có | Có | Không | Có |
| Có hai cặp cạnh đối diện song song | Không | Có | Có | Không | Có |
| Có hai cặp cạnh đối diện bằng nhau | Không | Có | Có | Không | Có |
| Có 4 góc vuông và 4 cạnh bằng nhau | Không | Không | Không | Không | Có |
| Có ít nhất 1 góc vuông | Không | Không | Có | Không | Có |
Giải vở bài tập Toán lớp 4 tập 2 trang 11 - Bài 3
Vẽ thêm hai đoạn thẳng để được một hình bình hành hoặc một hình chữ nhật
.png)
Đáp án
.png)
4. Bài tập tự luyện về hình bình hành
Câu 1: Tính diện tích hình bình hành có độ dài đáy là 12 cm và chiều cao 8 m.
Câu 2: Một mảnh đất hình bình hành có độ dài đáy là 35 dm và chiều cao là 25 dm. Tính diện tích của mảnh đất đó.
Câu 3: Một mảnh đất trồng hoa hình bình hành có độ dài đáy là 26 m và có chiều cao gấp đôi độ dài đáy. Tính diện tích mảnh đất trồng hoa đó.
Câu 4: Một tấm kính hình bình hành có chiều dài 280 mm và chiều cao 12 cm. Tính diện tích của tấm kính đó.
Câu 5: Một khu rừng dạng hình bình hành có chiều cao là 500 m, độ dài đáy gấp đôi chiều cao. Tính diện tích của khu rừng đó.
Câu 6: Một thửa ruộng hình bình hành có độ dài đáy là 100 m, chiều cao là 50 m. Người ta trồng lúa ở đó, tính ra cứ 100 m2 thu hoạch được 50 kg thóc. Hỏi đã thu hoạch được ở thửa ruộng đó bao nhiêu tạ thóc?
Bài 7: Tìm diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật BMNC, biết hình chữ nhật BMNC có chu vi bằng 18 cm và chiều dài MN gấp hai lần chiều rộng BM.
Bài 11: Một mảnh vườn dạng hình bình hành có tổng độ dài của chiều cao và độ dài đáy là 233 m, chiều cao kém độ dài đáy 17 m. Người ta trồng ngô trên mảnh vườn đó, tính ra cứ 100 m2 thì thu được 60 kg ngô. Hỏi đã thu hoạch được bao nhiêu tạ ngô trên mảnh vườn đó?
Bài 12: Một mảnh vườn hình bình hành có độ dài đáy 145 m, chiều cao kém độ dài đáy 29 m. Người ta dự định dùng 1/4 diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam. Hỏi diện tích đất trồng cam bằng bao nhiêu mét vuông?
Bài 14: Cho hình bình hành có:
a) Diện tích 135 cm2 và độ dài đáy 15 cm. Tính chiều cao của hình bình hành.
b) Diện tích 420 dm2 và chiều cao 3 m. Tính độ dài đáy của hình bình hành.
Baitap24h.com






