Trang 136 trong sách Toán lớp 4 giới thiệu phần "Luyện tập", giúp học sinh củng cố kiến thức đã học. Qua các bài tập phong phú, các em sẽ phát triển kỹ năng tính toán và tư duy phản biện, tạo nền tảng vững chắc cho những bài học tiếp theo.

Mục lục [Ẩn]
1. Lý thuyết phép chia phân số, phép nhân số
Phép chia phân số:
Để thực hiện phép chia hai phân số một cách đơn giản và hiệu quả, chúng ta tuân theo quy tắc cơ bản sau đây: lấy phân số thứ nhất và nhân nó với phân số thứ hai sau khi đã đảo ngược nó. Điều này có nghĩa là chúng ta giữ nguyên phân số đầu tiên và nhân nó với nghịch đảo của phân số thứ hai.
Để biểu diễn điều này một cách cụ thể hơn, giả sử chúng ta có phân số thứ nhất là a/b và phân số thứ hai là c/d. Để chia phân số a/b cho phân số c/d, ta thực hiện như sau:
1. Giữ nguyên phân số thứ nhất, tức là a/b.
2. Lấy nghịch đảo của phân số thứ hai, tức là d/c.
3. Nhân phân số thứ nhất với nghịch đảo của phân số thứ hai: (a/b) * (d/c).
Kết quả cuối cùng của phép tính này sẽ là phân số chia a/b cho c/d, và chúng ta có thể rút gọn kết quả nếu cần thiết. Điều này giúp chúng ta thực hiện phép chia hai phân số một cách dễ dàng và chính xác.
Phép nhân phân số:
Để thực hiện phép nhân hai phân số một cách đơn giản và hiệu quả, chúng ta tuân theo quy tắc cơ bản sau đây: trước hết, lấy tử số của phân số thứ nhất và nhân nó với tử số của phân số thứ hai. Sau đó, lấy mẫu số của phân số thứ nhất và nhân nó với mẫu số của phân số thứ hai.
Để biểu diễn điều này một cách cụ thể hơn, giả sử chúng ta có phân số thứ nhất là a/b và phân số thứ hai là c/d. Để nhân phân số a/b với phân số c/d, ta thực hiện như sau:
1. Lấy tử số của phân số thứ nhất, tức là a, và nhân nó với tử số của phân số thứ hai, tức là c.
2. Lấy mẫu số của phân số thứ nhất, tức là b, và nhân nó với mẫu số của phân số thứ hai, tức là d.
Kết quả cuối cùng của phép tính này sẽ là một phân số mới có tử số là a * c và mẫu số là b * d. Điều này giúp chúng ta thực hiện phép nhân hai phân số một cách dễ dàng và chính xác, giữ nguyên tính chất của phân số trong quá trình tính toán.
2. Làm thế nào để chia phân số?
Việc chia phân số có thể được phân loại thành ba cách khác nhau. họ đang
- Chia phân số cho một phân số
- Chia phân số cho số nguyên
- Chia phân số cho hỗn số
Chia phân số cho một phân số
Trong ba bước đơn giản, chúng ta có thể giải quyết phép chia phân số bằng cách chuyển thành phép nhân phân số. Hãy cùng chúng tôi tìm hiểu từng cái một.
- Viết nghịch đảo của phân số thứ hai và nhân nó với phân số thứ nhất
- Nhân tử số và mẫu số của cả hai phân số
- Đơn giản hóa số phân số
Nói chung, nếu a / b là phân số chia hết cho c / d. Sau đó, chúng ta có thể giải quyết sự phân chia như;
- a / b ÷ c / d = a / b × d / c
- a / b ÷ c / d = a × d / b × c
- a / b ÷ c / d = ad / bc
Bạn có thể thấy từ các biểu thức trên. A / b chia hết cho c / d thì chúng ta có thể viết thành a / b nhân với d / c (nghịch đảo của c / d). Và trong bước tiếp theo, chúng ta phải nhân cả tử số a & d và cả mẫu số, c & d. Do đó, chúng ta có thể đơn giản hóa việc tính toán phần còn lại.
Chia phân số cho một số nguyên
Trong khi chia các phân số với các số nguyên, quá trình chia rất dễ dàng. Làm theo quy trình dưới đây.
Bước 1: Tổng số được chuyển thành phân số bằng cách áp dụng giá trị của mẫu số là 1
Bước 2: Lấy nghịch đảo của số
Bước 3: Bây giờ, nhân giá trị phân số với một phân số đã cho
Bước 4: Đơn giản hóa biểu thức đã cho
Ví dụ: Chia 6/5 cho 10
Bước 1: Chuyển 10 thành phân số: 10/1
Bước 2: Lấy đối ứng: 1/10
Bước 3: Nhân 6/5 và 1/10: (6/5) × (1/10)
Bước 4: Đơn giản hóa: 3/25
Chia các phân số cho một phân số hỗn hợp
Quá trình chia một phân số cho một phân số hỗn hợp có thể được thực hiện gần giống như phép chia phân số cho một phân số thông thường. Trong cả hai trường hợp, chúng ta cần lấy phân số thứ nhất (dividend) và chia nó cho phân số thứ hai (divisor). Tuy nhiên, khi divisor là một phân số hỗn hợp, chúng ta cần chuyển đổi nó thành phân số trước khi thực hiện phép chia.. Các bước để thực hiện phép chia một phân số cho một phân số có hỗn số như sau:
Bước 1: Chuyển phân số hỗn hợp thành phân số không đúng
Bước 2: Bây giờ, lấy nghịch đảo cho phân số không đúng
Bước 3: Nhân phân số thu được với phân số đã cho
Bước 3: Đơn giản hóa các phân số
Ví dụ: Chia ⅖ cho 3½.
Bước 1: Chuyển 3½ thành một phân số không đúng, ta được 7/2
Bước 2: Lấy nghịch đảo cho phân số không đúng: 2/7
Bước 3: Nhân ⅖ và 2/7
Bước 4: Đơn giản hóa: 4/35
3. Toán lớp 4 trang 136: Luyện tập có đáp án chi tiết nhất
Toán lớp 4 trang 136 luyện tập Bài 1


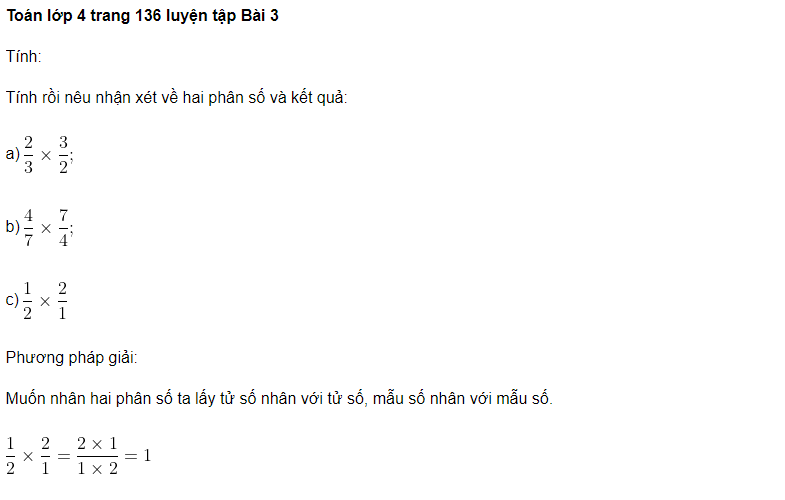
Nhận xét:
Trong mỗi phép nhân hai phân số, chúng ta luôn gặp phải sự kỳ diệu khi hai phân số đó là hai phân số đảo ngược nhau. Điều này có nghĩa là nếu chúng ta có phân số thứ nhất là a/b và phân số thứ hai là b/a, thì chúng ta đang xử lý hai phân số đảo ngược lẫn nhau.
Một điều thú vị là tích của hai phân số đảo ngược luôn bằng 1. Điều này có thể dễ dàng kiểm tra bằng cách thực hiện phép nhân. Nếu chúng ta nhân phân số a/b với phân số b/a, kết quả sẽ là (a/b) * (b/a), và chúng ta có thể thấy rằng b và a sẽ đối nghịch và loại bỏ lẫn nhau. Kết quả cuối cùng sẽ là 1, luôn đồng nghĩa với một.
Điều này là một trong những tính chất thú vị và quan trọng của các phân số, và nó giúp chúng ta hiểu rõ hơn về cách các phân số tương tác trong các phép tính toán.
Toán lớp 4 trang 136 luyện tập Bài 4

4. Bài tập phép chia phân số lớp 4


Baitap24h.com






