Trong chương trình Toán lớp 4, bài 107 mang đến cho học sinh một thử thách thú vị về việc so sánh hai phân số. Việc nắm vững kỹ năng này không chỉ giúp học sinh hiểu rõ hơn về phân số mà còn nâng cao khả năng tư duy logic, giúp các em áp dụng vào thực tiễn cuộc sống.

Mục lục [Ẩn]
1. Câu 1 - Vở bài tập toán lớp 4 Bài 170
Điền dấy (>, =, <) vào chỗ trong dưới đây:

Phương pháp giải:
Phương pháp giải bài toán so sánh giữa hai phân số khi chúng có cùng mẫu số là một quy tắc cơ bản và quan trọng trong toán học. Cụ thể, phương pháp giải đối với dạng toán này như sau:
- Tử số bé hơn đồng nghĩa với phân số bé hơn: Nếu một phân số có tử số nhỏ hơn phân số kia, thì ta có thể kết luận rằng phân số đó nhỏ hơn. Điều này dễ hiểu vì khi mẫu số giống nhau, tử số càng lớn thì giá trị của phân số càng cao.
- Tử số lớn hơn đồng nghĩa với phân số lớn hơn: Nếu một phân số có tử số lớn hơn phân số kia, thì chúng ta có thể khẳng định rằng phân số đó lớn hơn. Điều này là do tử số lớn hơn đồng nghĩa với việc phần chia của phân số đó có giá trị cao hơn.
- Tử số bằng nhau đồng nghĩa với phân số bằng nhau: Trong trường hợp cả hai phân số có tử số bằng nhau, chúng ta có thể kết luận rằng chúng bằng nhau. Điều này là do tử số là yếu tố quyết định giá trị tuyệt đối của phân số khi mẫu số giống nhau.

2. Câu 2 - Vở bài tập toán lớp 4 Bài 170
Điền dấu (>, =, <) vào chỗ chấm:

Phương pháp giải:
- Tử số bé hơn mẫu số đồng nghĩa với phân số bé hơn 1: Khi tử số của một phân số nhỏ hơn mẫu số, chúng ta có thể hiểu rằng giá trị của phần chia (tổ) là nhỏ hơn mẫu số. Do đó, phân số này sẽ nằm trong khoảng từ 0 đến 1. Ví dụ, nếu có phân số , tử số 4 nhỏ hơn mẫu số 5, do đó phân số này bé hơn 1.
- Tử số lớn hơn mẫu số đồng nghĩa với phân số lớn hơn 1: Ngược lại, khi tử số lớn hơn mẫu số, tức là giá trị của phần chia cao hơn mẫu số, phân số này sẽ lớn hơn 1. Chẳng hạn, với phân số , tử số 8 lớn hơn mẫu số 7, cho thấy phân số này lớn hơn 1.
- Tử số bằng mẫu số đồng nghĩa với phân số bằng 1: Trong trường hợp tử số bằng mẫu số, chúng ta kết luận rằng giá trị của phần chia là bằng nhau với mẫu số, và phân số này sẽ bằng 1. Chẳng hạn, phân số có tử số bằng mẫu số là 6, do đó phân số này tương đương với số 1.
Đáp án:

3. Câu 3 - Vở bài tập toán lớp 4 Bài 170
Viết các phân số bé hơn 1, có mẫu số là 8 và có tử số khác 0
Phương pháp giải:
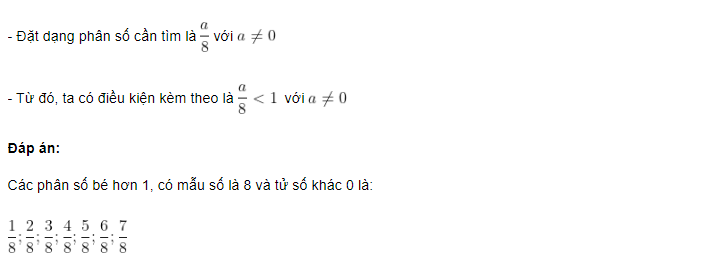
4. Câu 4 - Vở bài tập toán lớp 4 Bài 170
Sắp xếp các phân số sau: theo thứ tự từ lớn đến bé
Phương pháp giải:
- So sánh và sắp xếp từ bé đến lớn: Bước đầu tiên là so sánh các phân số và sắp xếp chúng theo thứ tự tăng dần. Điều này giúp chúng ta có cái nhìn tổng quan về sự biến đổi giữa các giá trị của các phân số và làm cho quá trình so sánh trở nên dễ dàng hơn.
- Áp dụng cách so sánh với cùng mẫu số: Sau đó, chúng ta chuyển sang cách so sánh hai phân số cùng mẫu số. Các quy tắc so sánh này giúp chúng ta xác định mối quan hệ giữa các phân số một cách chi tiết:
Nếu tử số của một phân số nhỏ hơn, phân số đó sẽ bé hơn.
Nếu tử số của một phân số lớn hơn, phân số đó sẽ lớn hơn.
Trong trường hợp tử số bằng nhau, chúng ta kết luận rằng hai phân số đó là bằng nhau.
- Kết hợp so sánh và sắp xếp: Khi đã có kết quả từ bước so sánh theo mẫu số, chúng ta có thể kết hợp với việc sắp xếp để thu được danh sách các phân số đã được sắp xếp từ bé đến lớn. Điều này giúp làm rõ hơn về thứ tự tương đối giữa chúng.
Đáp án:

5. Lý thuyết cần nắm vững khi làm bài tập so sánh hai phân số cùng mẫu số
Trong quá trình nghiên cứu và giải quyết bài toán về phân số, chúng ta có thể mở rộng sự hiểu biết về quy tắc so sánh và tương quan giữa tử số và mẫu số trong môi trường phức tạp hơn. Dưới đây là một phân tích chi tiết về các quy tắc và tính chất của phân số, không chỉ tập trung vào so sánh mà còn nhấn mạnh vào sự tương quan giữa tử số và mẫu số:
- So sánh trong cùng mẫu số: Khi hai phân số có cùng mẫu số, chúng ta có thể dễ dàng so sánh chúng bằng cách quan tâm đến giá trị của tử số. Nếu tử số của một phân số nhỏ hơn phân số kia, thì chúng ta kết luận rằng phân số đó nhỏ hơn. Ngược lại, nếu tử số lớn hơn, phân số đó lớn hơn.
- Tương quan với giá trị tuyệt đối và số 1: Khi tử số bé hơn mẫu số, chúng ta nhận thấy phân số đó nhỏ hơn 1. Điều này là do giá trị tuyệt đối của tử số là một phần nhỏ hơn giá trị tuyệt đối của mẫu số, tạo ra một giá trị phân số nằm trong khoảng từ 0 đến 1. Ngược lại, khi tử số lớn hơn mẫu số, phân số sẽ lớn hơn 1.
- Đặc điểm của sự bằng nhau: Trong trường hợp tử số bằng nhau, chúng ta không chỉ xác nhận sự bằng nhau giữa hai phân số mà còn có thể chú ý đến sự tương quan giữa tử số và mẫu số. Nếu tử số bằng mẫu số, chúng ta có phân số bằng nhau với giá trị là 1.
Qua quá trình này, ta không chỉ hiểu rõ về cách so sánh giữa các phân số mà còn nhận thức về sự liên quan giữa tử số và mẫu số đối với giá trị tuyệt đối và số 1. Điều này giúp chúng ta áp dụng kiến thức về phân số một cách linh hoạt và sâu sắc hơn trong việc giải quyết nhiều loại bài toán và hiểu rõ hơn về bản chất của chúng trong toán học.
6. Bài tập ôn tập thêm
Bài tập 1: Nhận định sau là đúng hay sai: Có 02 phân số (khác 0) có mẫu số bằng nhau, phân số nào có tử số bé hơn thì phân số đó lớn hơn ?
A. Đúng
B. Sai
Đáp án:
Trong quá trình thực hiện các phép so sánh giữa hai phân số có cùng mẫu số, chúng ta thường dựa vào giá trị của tử số để xác định mối quan hệ giữa chúng. Theo đó, áp dụng nguyên tắc khi so sánh 02 phân số có cùng mẫu số như sau:
- Tử lớn hơn thì phân số đó lớn hơn
- Từ bé hơn thì phân số đó bé hơn
- Từ bằng nhau thì 02 phân số bằng nhau
Do đó, nhận định nêu trên là Sai. Phương án đúng cần chọn là B.
Bài tập 2: Phân số nào dưới đây lớn hơn



Bài tập 5: Không quy đồng phân số, hãy so sánh các phân số sau:
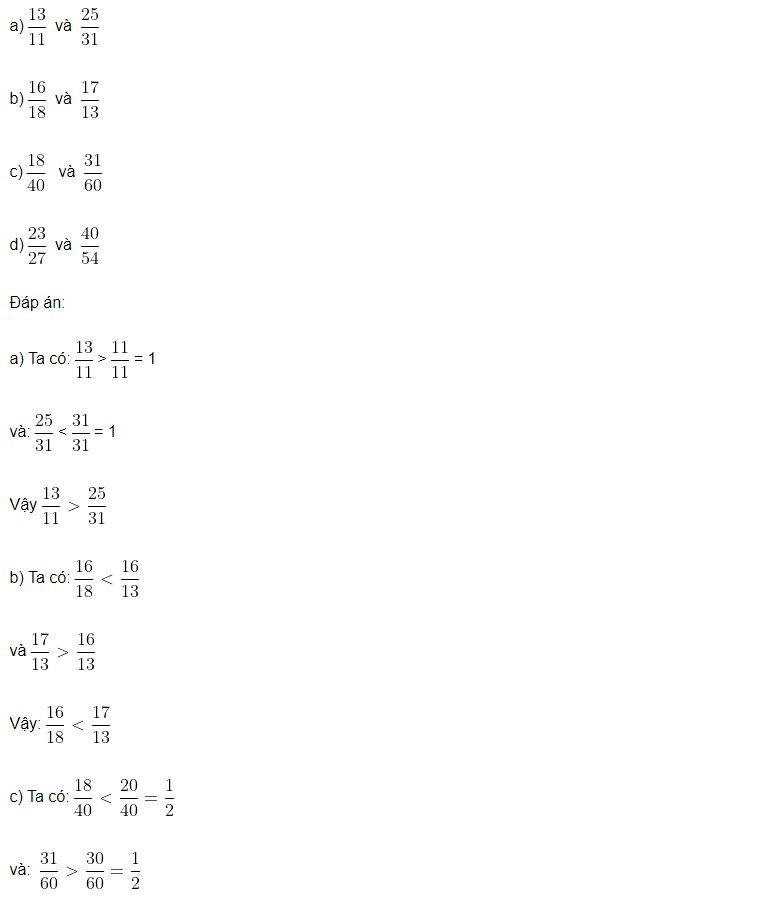


Baitap24h.com






